Working together
with foundations
that care.
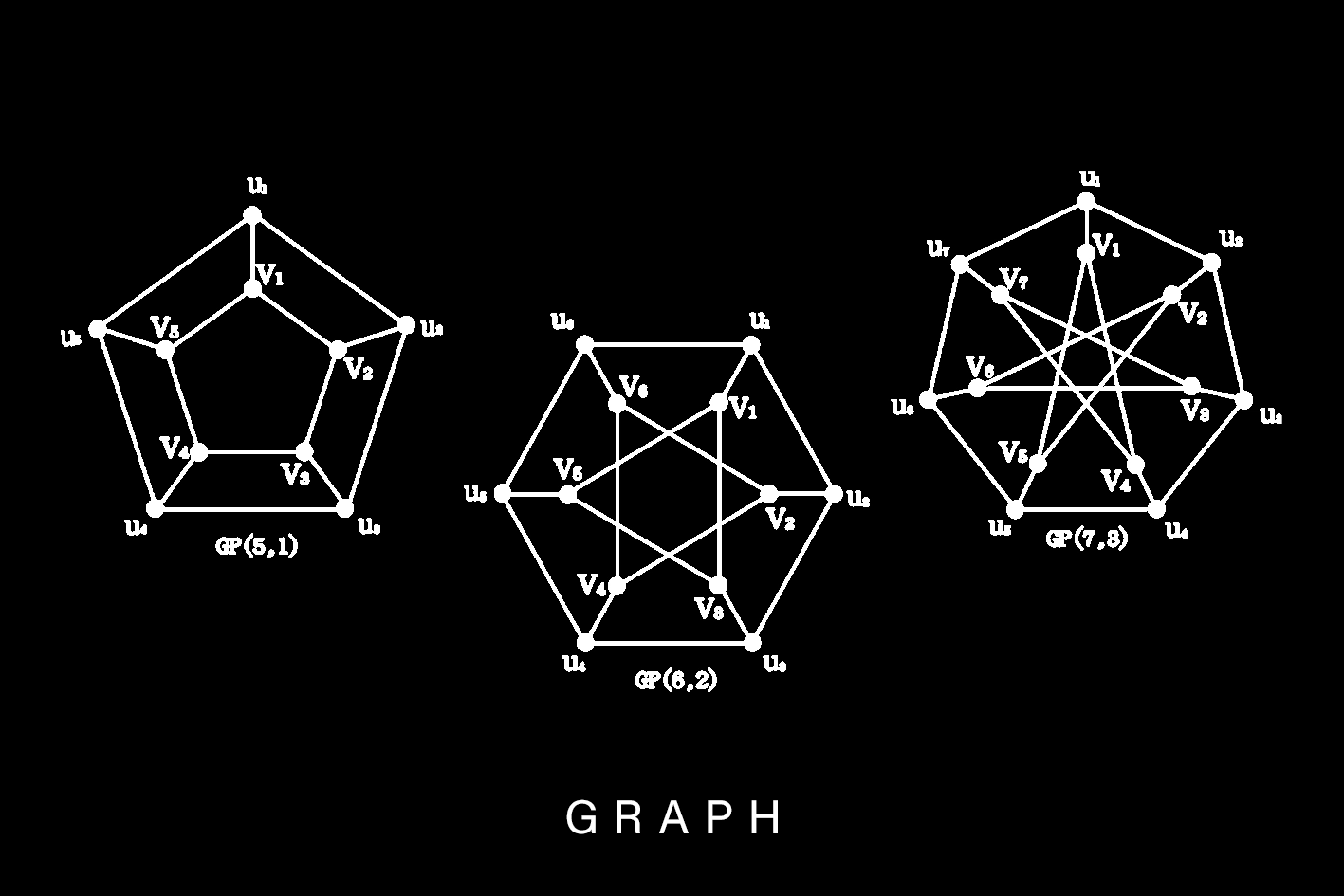
Combinatorics and Graph Theory are extremely important to
model discrete systems, counting sequences and are an
important basis for logistics modelling and the learning of
Graph Neural Networks.
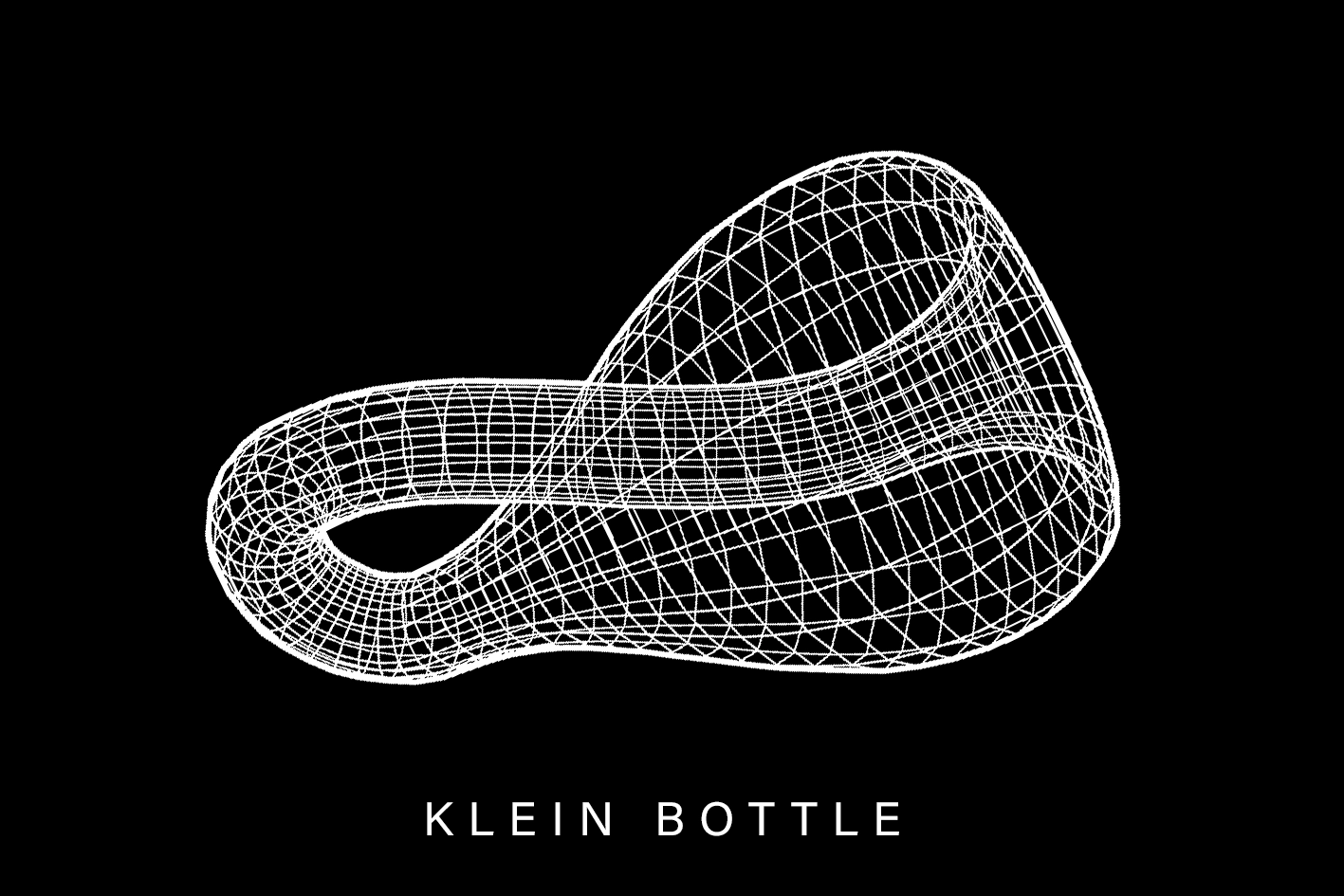
Differential Geometry enables the study of geometric
objectics using calculus. So not only position or velocity but
also shape, curvature and overall geometry of spaces. This can
be highly used to derive embedding models for reducing
dimensionality and therefore the complexity of problems and
also learn the manifold structure of the loss function we are
studying when trying to optimize a certain model based on
that loss function.
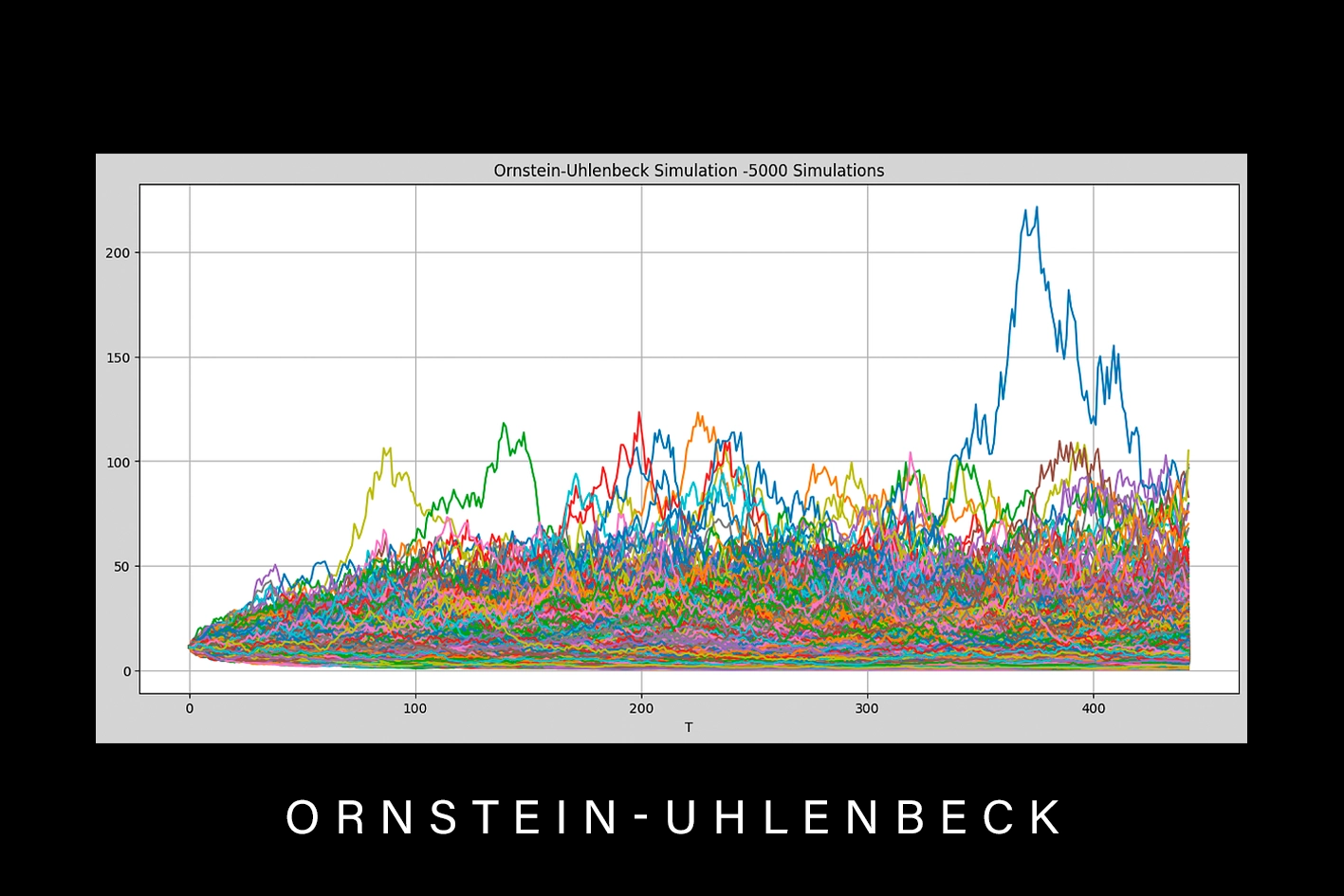
Time Series, Financial Mathematics and Optimization in
Finance give the tools for modelling financial instruments and
derive high precision models for time series.
Computational Complexity, Computability Theory and
Probabilistic Methods in Computer Science are king for
finding simple, efficient and fast models which take
advantage of the probabilistic sampling algorithms to derive
not only one but thousands of different learners that yield final
models with higher confidence while enabling uncertainty
calculation.
Partial Differential Equations are used to model how physical
quantities such as position, velocity, temperature, pressure or
even probability density change continuously in space and
time.